Spatial beam self-cleaning, a recently discovered nonlinear optical effect that occurs in multimode fibers (MMFs) with gradient index (GRIN) profile [1, 2], has fundamental significance and potential important applications to high power beam delivery and fiber lasers. Spatial beam self-cleaning results from a complex spatio-temporal beam dynamics, driven by the interplay of random mode coupling and the intensity dependent contribution to the refractive index, or Kerr effect. Beam self-cleaning leads to the formation at the MMF output of a highly stable, spatially compressed beam with a diameter close to that of fundamental fiber mode. Typically, spatial self-cleaning is observed in several meters of GRIN MMF at threshold power levels of the order of few kWs, orders of magnitude lower than the value for catastrophic self-focusing, and lower than the stimulated Raman scattering (SRS) threshold. So far, although different qualitative explanations have been provided [1, 3, 4], the physical mechanism leading to Kerr beam cleaning remains largely debated.

In this work, we numerically and experimentally demonstrate a fascinating similarity between spatial beam selfcleaning in MMFs and hydrodynamic 2D turbulence. Here a large-scale condensate results from parametric instabilities, which generate a number of nonlinearly interacting modes with randomized phases, followed by a direct and inverse spectral cascade [5].

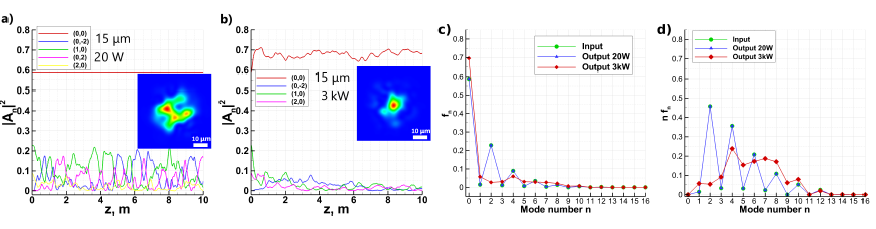
Kerr beam cleaning is a two-step physical process. First, above a certain input power threshold, parametric instability among the spatial modes leads to a net power transfer from low-order modes (LOMs) towards the fundamental mode of the fiber. This process is accompanied, for symmetry reasons, by a power transfer towards HOMs, while leaving the average mode number unchanged. We analytically predict such power threshold, by approximating the mode coupling process with a truncated three-mode expansion. For a quantitative comparison with experiments, we performed extensive numerical simulations based on full coupled-mode equations. We consider that only modes with the same mode numbers n are linearly coupled, and that each element of the coupling matrix C is normally distributed with zero mean, and varies randomly along the fiber with a correlation length of 10 cm. As initial data, we used a Gaussian beam of a given radius, which was decomposed into modes, thereby setting the initial modal power distribution.

In our simulations, we only considered spatial modes with mode number n 16 (for a total of 153 modes). As shown in Fig. 1, power transfer occurs between a large number of nonlinearly interacting modes with randomised phases, leading to optical wave turbulence. Cascaded four-wave mixing redistributes the input beam power away from LOMs, towards HOMs (direct cascade) and the fundamental mode (inverse cascade). The second step of self-cleaning is the nonlinear nonreciprocity-induced irreversible decoupling of the fundamental mode from HOMs [1].

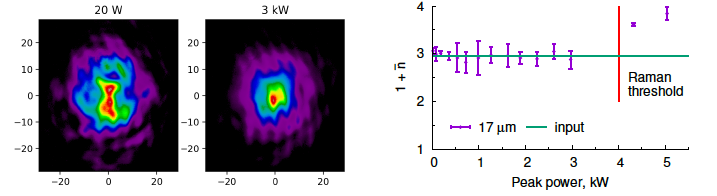
In the experiment, we launched into a 10-m-long GRIN MMF intense laser pulses from a micro-chip Nd:YAG laser with a duration of 0.6 ns and a wavelength of 1064 nm. Using a 62.5 μm core fiber, in combination with a beam expander that allowed us for a continuous change of the input beam radius from 15 to 32 μm, we found that the establishment and stability of self-cleaning effect is strongly dependent of the initial beam parameters. For an input beam radius of 17( 1) μm, the speckled structure observed at low powers transforms, at powers >1 kW, into a bright spot (Fig. 2, left) that is totally insensitive to fiber deformations.

Our main result is the experimental confirmation of the conservation of the average mode number in the process of beam self-cleaning. This condition characterizes the simultaneous occurrence of inverse and direct energy cascade in hydrodynamic 2D turbulence [5]. In Fig. 2, right, we show the measured dependence of the average mode number on output peak power: as can be seen, below the SRS threshold the input average mode number is conserved, in excellent agreement with the theoretical values (solid curve). Our results provide yet another demonstration of the interdisciplinary links between hydrodynamic and optical turbulence, and the universality of pattern generation mechanisms in different physical settings.

1. K. Krupa, A. Tonello, B. M. Shalaby, M. Fabert, A. Barth´el´emy, G. Millot, S.Wabnitz, and V. Couderc, ”Spatial beam self-cleaning in multimode fibres,” Nat. Photonics 11, 237–241 (2017).
2. Z. Liu, L.G. Wright, D.N. Christodoulides, and F.W.Wise, ”Kerr self-cleaning of femtosecond-pulsed beams in graded-index multimode fiber,” Opt. Lett. 41, 3675-3678 (2016).
3. P. Aschieri, J. Garnier, C. Michel, V. Doya, and A. Picozzi, ”Condensation and thermalization of classical optical waves in a waveguide,” Phys. Rev. A, 83 033838 (2011).
4. L.G. Wright, Z. Liu, D.A. Nolan, M.-J. Li, D.N. Christodoulides, and F.W. Wise, ”Self-organized instability in graded-index multimode fibres,” Nature Photonics 10, 771-776 (2016).
5. R. H. Kraichnan, Phys. Fluids 10, 1417 (1967), ”Inertial ranges in two-dimensional turbulence,” Phys. Fluids 10, 1417 (1967).