Finding spatiotemporal light bullets in multicore and multimode fibers
An interesting phenomenon associated with multicore fibers (MCFs) and multimode fibers (MMFs) is the generation of light bullets – high-energy pulses localized both in time and space, and propagating without distorting their shape along the fiber. Light bullets are formed due to the mutual compensation of diffraction, anomalous dispersion, and nonlinearity; they were recently observed in experiments [1-3]. In bulk media, small fluctuations in the intensity or width of the light beam can lead to collapse; in such case, light bullets are unstable. However, in discrete media, such as for example in MCFs, a similar effect is not observed [4]. In recent years, due to the increased interest in multicore light guides, many papers have appeared which are devoted to theoretical studies of light bullets. The propagation of the electromagnetic field in multicore and multimode fibers can be described by a system of coupled nonlinear Schrödinger equations (CNLSEs) or generalized Manakov equations Approximate analytical solutions in the form of space-time discrete solitons can be obtained for models of centrally symmetric multicore optical fibers based on the CNLSEs.
But in most cases, the search for stationary solutions of pulse propagation in MCFs and MMFs is only possible with the help of numerical methods. Here we consider the case of a MCF with a centrally symmetric arrangement of the cores. Since the central core introduces an irregularity into the structure, the use of standard iterative methods for finding a stationary solution in the form of a light bullet of nonzero energy is difficult in this situation.
In this work, we introduce a new two-level iterative algorithm, which allows for numerically finding a pulsed stationary solution of the CNLSEs with different types of couplings among the cores of the MCF. The propagation of the found solutions was simulated, in order to demonstrate truly stationary dynamics. Next, we derive a new approximate analytical solution for ring MCFs with central core, and demonstrate the stability of such a solution. In addition, the analytical solution can also be used as initial distribution in order to start the iterative algorithm. Finally, we briefly investigate spatiotemporal bullet solutions for MMFs.
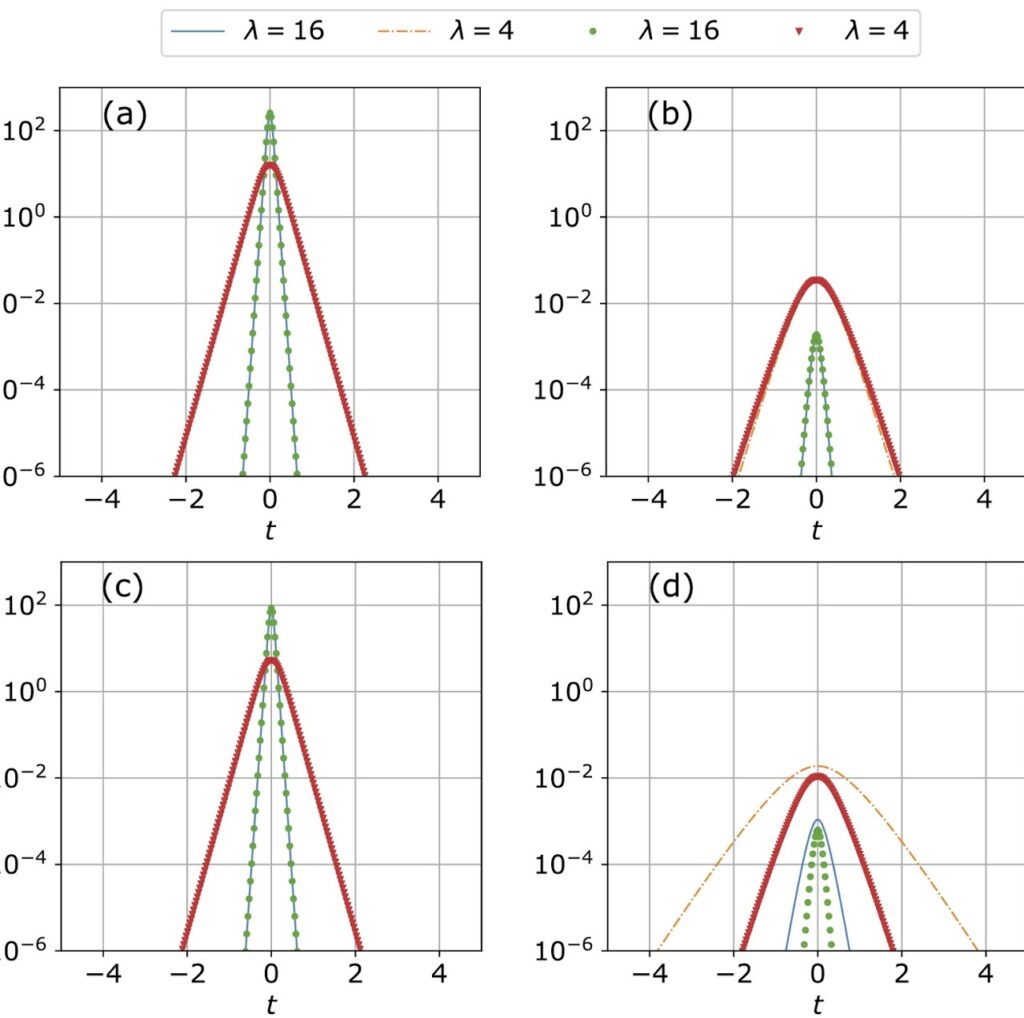
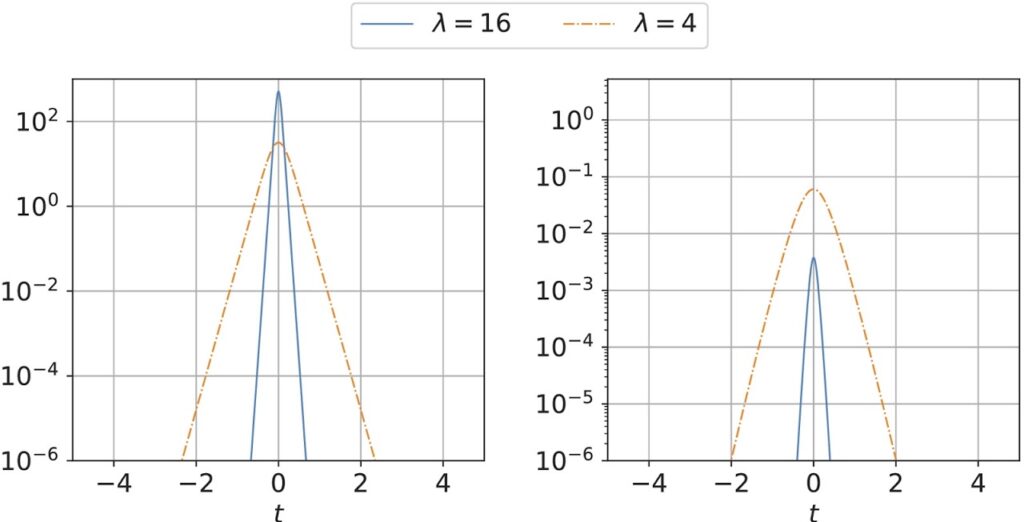
We carried out a comparative analysis of our analytical approximate and numerical solutions of the CNLSEs. In Fig. 1 we illustrate the results of the comparison of the obtained pulse profiles in the central (a,c) and peripheral (b,c) cores, for different values of the parameter 𝜆 (square root of the wavenumber), and for core numbers 𝑁𝑐=2 and 𝑁𝑐=6, respectively. In the central core, a good agreement between analytical and numerical solutions is observed, both in amplitude and in pulse width. The relative error of the discrepancy among approximate analytical and numerical solutions was ≈10−3. Note that the case with 𝑁𝑐=6 peripheral cores can be considered as a 7-core hexagonal MCF also. For the peripheral cores, a good agreement is only observed in amplitude, for small values of the parameter 𝜆; whereas a slight discrepancy in the pulse widths is obtained.
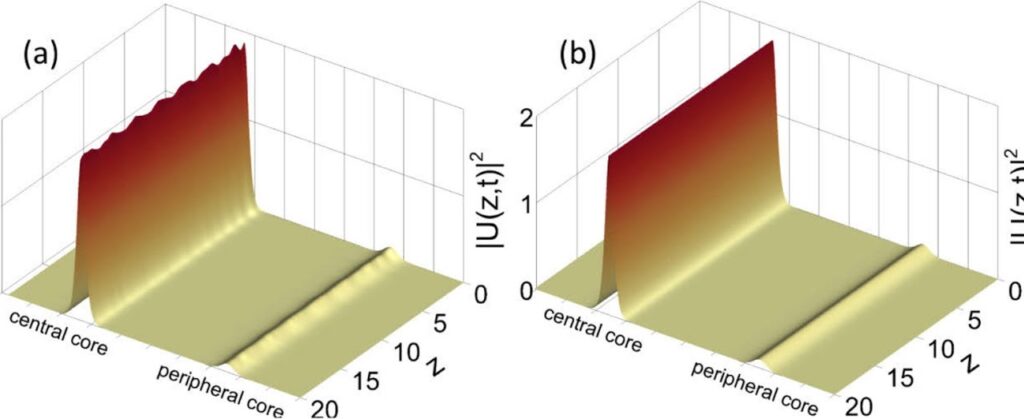
Figure 2 presents an example of propagation of the analytic solution and of the numerical solution. The analytical solutions can give adequate approximation of numerical solutions in many cases.
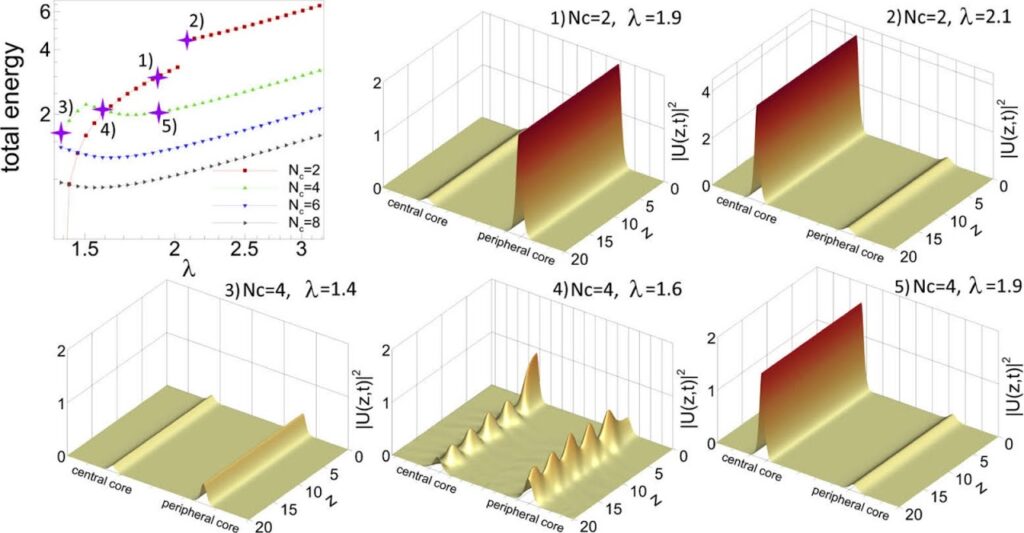
WEe found that all stationary solutions for 𝑁𝑐=2 are stable, and can propagate without a shape change. On the other hand, for 𝑁𝑐≥4, a value 𝜆𝑠=𝜆𝑠(𝑁𝑐) exist, such that the solution obtained for 𝜆∗<𝜆<𝜆𝑠 is unstable. Figure 3 illustrates this observation. In the top left panel of Fig. 3, we pointed out by stars on the total energy 𝐸=𝐸(𝜆,𝑁𝑐) curve some specific solutions and drew the corresponding pulse dynamics along fiber length 𝑧. Solutions 1) and 2) correspond to the distributed and soliton stationary regimes for a MCF with 𝑁𝑐=2 peripheral cores. Both solutions are stable due to the Vakhitov-Kolokolov criterion, and propagate without change of shape in numerical simulations performed by the split-step Fourier method adapted for CNLSEs. Solutions 3) – 5) belong to different ranges of the parameter 𝜆. Regime 5) is a stable soliton solution, while regime 4) corresponds to an unstable soliton solution, since the Vakhitov-Kolokolov criterion is not met in this case. Nevertheless, the dynamics of regime 4) show that for a given value of 𝜆there is a stable distributed solution that was not captured by the algorithm, due to insufficiently close initial data. Finally, solution 3) belongs to a family of stable distributed solutions.
The proposed two-level algorithm can also be applied to systems describing optical pulse propagation in MMFs. We consider two coupled equations for the number of photons in the fundamental mode and the generic higher-order-mode (HOM), respectively, where 𝐾 is a constant coupling coefficient originating from nonlinear four-wave mixing terms. Figure 4 presents the corresponding stationary bullet solutions.
- F. Eilenberger, S. Minardi, A. Szameit, U. Röpke, J. Kobelke, K. Schuster, H. Bartelt, S. Nolte, A. Tünnermann, and T. Pertsch, “Light bullets in waveguide arrays: spacetime-coupling, spectral symmetry breaking and superluminal decay [Invited],” Opt. Express 19(23), 23171 (2011).
- W. H. Renninger and F. W. Wise, “Optical solitons in graded-index multimode fibres,” Nat. Commun. 4(1), 1719 (2013).
- P. Panagiotopoulos, P. Whalen, M. Kolesik, and J. V. Moloney, “Super high power mid-infrared femtosecond light bullet,” Nat. Photonics 9(8), 543–548 (2015)
- A. B. Aceves, A. M. Rubenchik, S. K. Turitsyn, and C. De Angelis, “Multidimensional solitons in fiber arrays,” Opt. Lett. 19(5), 329–331
