Kerr-lens mode-locking (KLM) [1] provided unprecedented progress in the generation of ultrashort pulses in solid-state oscillators, with remarkable fundamental and practical consequences [2]. KLM utilizes self-focusing inside a nonlinear medium, which causes an effective loss decrease with power growth. This involves using the inherent nonlinearity of a dissipative system for producing highly coherent localized structures (i.e., dissipative solitons, or DSs). Simultaneously, a remarkable breakthrough has been achieved by introducing ultrafast fiber lasers, which permit to avoid thermal effects and environmental sensitivity issues, while providing high gains and covering a broad spectral range [2]. However, optical nonlinearities limit energy harvesting in ultrafast fiber lasers. The typical method to suppress nonlinearity by means of increasing the mode-size may results in multimode instabilities [3]. Nevertheless, current studies have demonstrated that the introduction of distributed nonlinearity, in combination with a careful control of dissipative effects, could allow for stable energy harvesting (by means of the so-called distributed KLM, DKLM mode of operation) [4]. As a result, spatiotemporal mode-locking (ML) in both solid-state and fiber lasers could be realized [3, 5–6].

In this work, we demonstrate, for the first time to our knowledge, that the transversely-graded dissipation provided by doping of a graded-index (GRIN) fiber allows for DKLM in a fiber laser, operating in either the anoma- lous or the normal group-delay dispersion (GDD) regime (ANDR and NDR), respectively. We investigate, both analytically and numerically, the parameters and stability of spatiotemporal DSs. The problem of ML self-starting, and the outlook for the experimental demonstration of fiber DKLM are discussed.

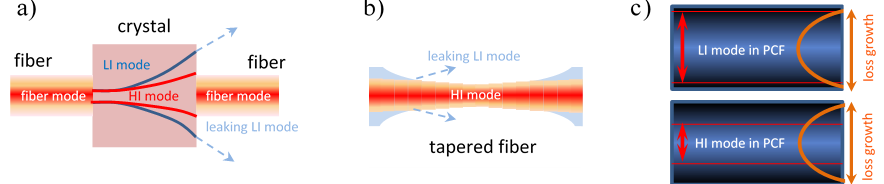
As was discussed broadly, the trapping parabolic-like profile of the refractive index in a GRIN fiber assists spa- tiotemporal soliton stabilization [3]. Here we propose using a gradient-gain-profile in a doped fiber amplifier. This produces a distributed amplification, akin to the action of an aperture in a KLM oscillator (see Fig.1). As a result, we pre- dict the formation of a stable spatiotemporal DS in an all-fiber laser, without any additional ML mechanism, thus implementing fiber-based DKLM. We consider a GRIN fiber with axially symmetrical parabolic profile of the refractive index (s). In combination with GDD (δ) and Kerr-nonlinearity (ν), propagation of the laser field a can be described by the Gross-Pitaevskii equation [3], generalized with taking into account of the net-loss, including saturated gain on the fiber axis (Λ), spectral dissipation (τ), and parabolic profiled loss (κ).

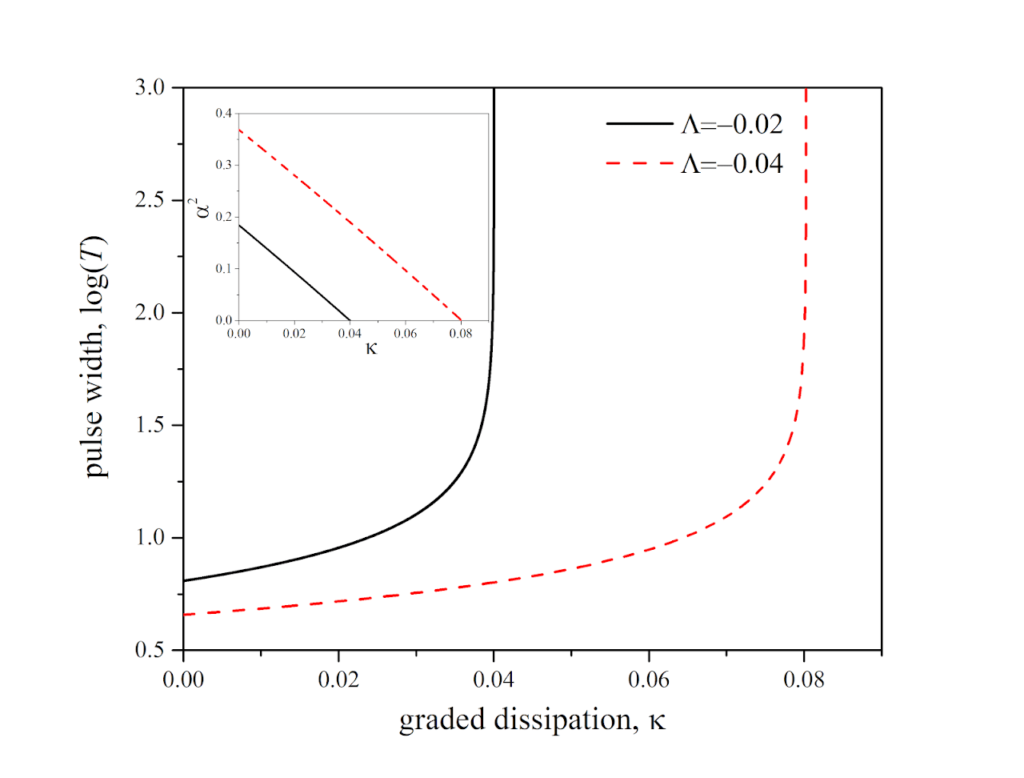
Our model admits an analysis based on the variational approximation in combination with the Kantarovich’s method, taking into account dissipative factors. The obtained results are briefly summarized in Figs.1-2. Fig. 2 shows the dependencies of the DS temporal width and peak power on the graded dissipation parameter κ for the case of normal-GVD are shown in Fig. 2. A DS is positively chirped for both anomalous- and normal-GVD regimes (ψ > 0), and it has a negative wave-front curvature (θ < 0).

On the other hand, Fig.3 shows the dependence of DS stability boundaries on the “relative aperture size” χ = ^􏰄|Λ|/κ. This defines the size of the dissipative guiding window and the graded-loss coefficient κ, for both ANDR and NDR regimes.

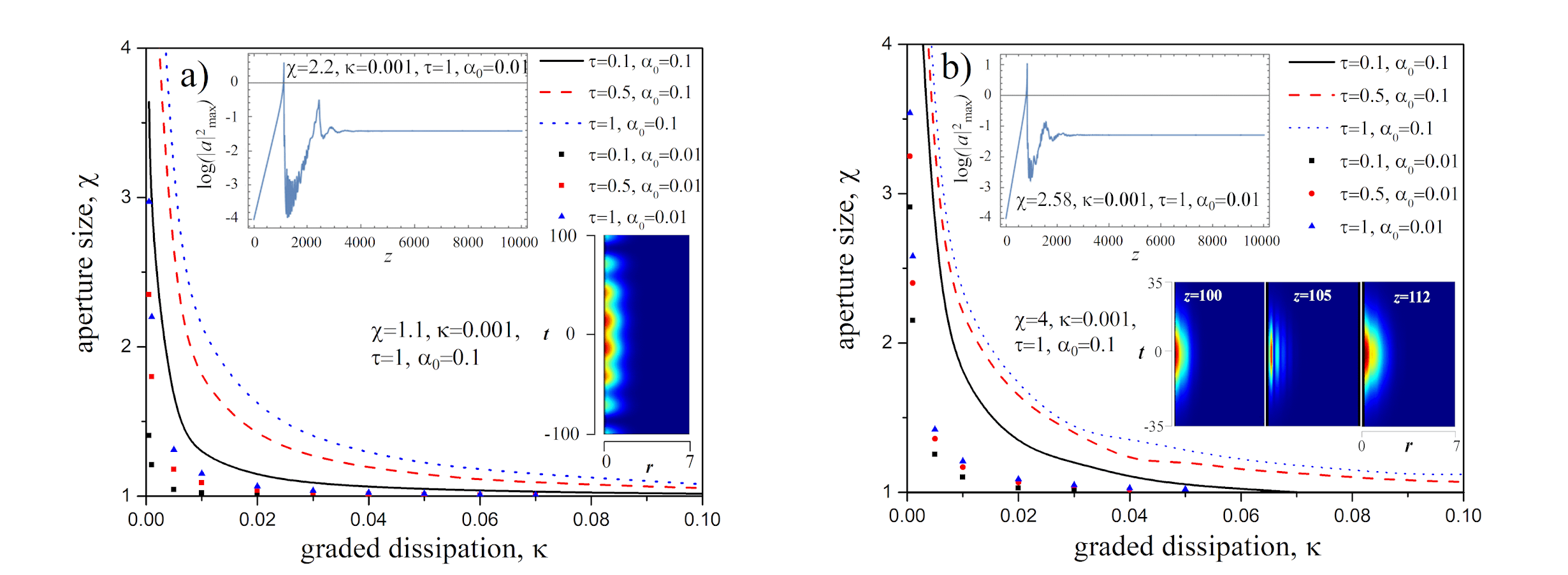
Our principal results can be summarized in the following way. i) Spectral dissipation enhances DS stability, and broadens the “attraction basin,” i.e., the ML self-starting ability, which is not possible for τ = 0. ii) The growth of the graded-dissipation index κ reduces the stability region, and increases the DS duration. However, it also reduces the sensitivity to the initial condition, which could mean an enhancement of the ML self-starting ability. iii) The DS stability region is broader for the case of NDR. Direct numerical simulations demonstrate the self-starting of DS generation for both regimes, as well as the contribution of higher-order modes, causing DS oscillations (insets in Fig. 3, b). The main destabilizing scenarios are provided by i) multipulsing in the ANDR (inset in Fig. 3, a), ii) DS collapse in the NDR, owing to strong Q-switching on the initial stage of ML, and iii) unlimited temporal spreading of the DS.

We anticipate that the nonlinear coupling of spatial modes in both GRIN and photonic-crystal fibers could lead implementing DKLM in a fiber laser in the regime of multimode self-cleaning [3] supported by the graded dissipation, thus providing highly-efficient and stable energy harvesting in an all-fiber laser, without using any additional ML mechanism (i.e., a self-ML is realized).

1. D. E. Spence, et al., “60-fsec pulse generation from a self-mode-locked Ti:sapphire laser,” Opt. Lett. 16, 42–44 (1991).
2. see chapters in Ultrafast Lasers: Technology and Applications, M. E. Fermann, A. Galvanauskas, G. Sucha, eds. (Marcel Dekker, 2003).
3. K. Krupa, et al., “Multimode nonlinear fiber optics, a spatiotemporal avenue,” APL Photonics 4, 110901 (2019).
4. J. Zhang, et al., “Generation of 49-fs pulses directly from distributed Kerr-lens mode-locked Yb:YAG thin- disk oscillator,” in Advanced Solid State Lasers Conference, OSA Technical Digest (online) (Optical Society of America, 2015), paper ATh4A.7.
5. W. H. Renninger, F. W. Wise, “Spatiotemporal soliton laser,” Optica 1, 101–104 (2014).
6. L. G. Wright, et al., “Spatiotemporal mode-locking in multimode fiber lasers,” Science 358, 94–97 (2017).