Multimode optical fibers (MMFs) have recently regained interest because of the degrees of freedom associated with their different eigenmodes. In the nonlinear propagation regime in particular, new phenomena have been unveiled in graded-index (GRIN) MMFs such as geometric parametric instabilities and Kerr beam self-cleaning. The speckled pattern observed at the output of the MMF at low powers, is transformed at high powers into a bell-shaped beam close to the fundamental mode. Recent work has also demonstrated that Kerr beam self- cleaning can lead to a low-order spatial mode, different from a bell-shape, by adjusting the laser beam in-coupling conditions. An attractive way to systematically control the spatial excitation conditions at the fiber input is provided by the use of a spatial light modulator (SLM) which permits to profile the beam wavefront entering the MMF. In most cases, experiments involving adaptive optics consider linear propagation through scattering plates or MMFs [1]. So far, few works have dealt with the nonlinear propagation regime[2,3].

In this work, we report experiments showing the control at high powers of the transverse output pattern of a 5 meters long 52/125μm GRIN-MMF. We may thus control, with the contribution of Kerr nonlinearity within an adaptive loop, the stable generation of a few transverse eigenmodes. A deformable mirror with 12×12 actuators shapes the input wavefront of the laser beam at 1064nm, carrying 7ps pulses at 1MHz repetition rate.

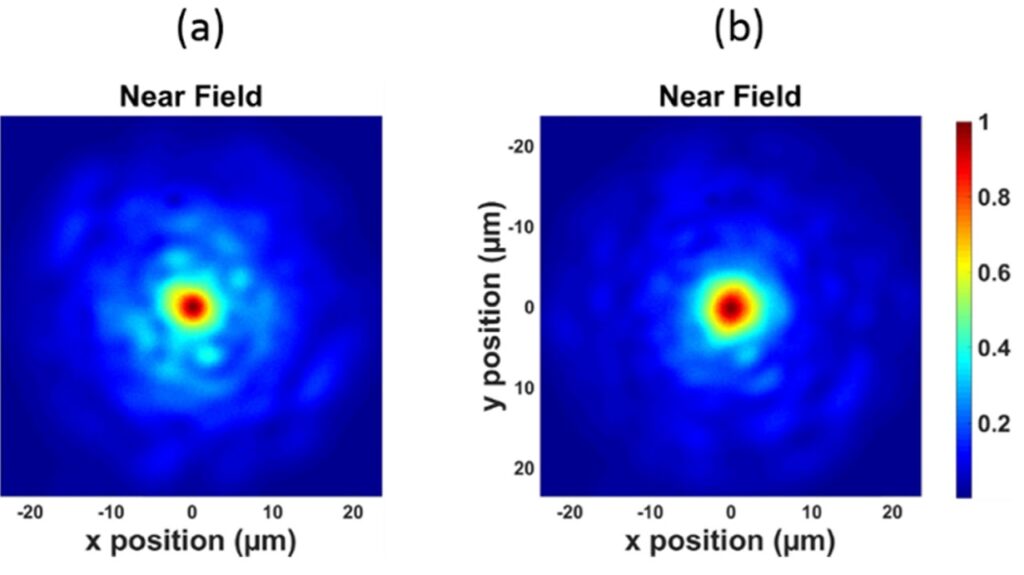
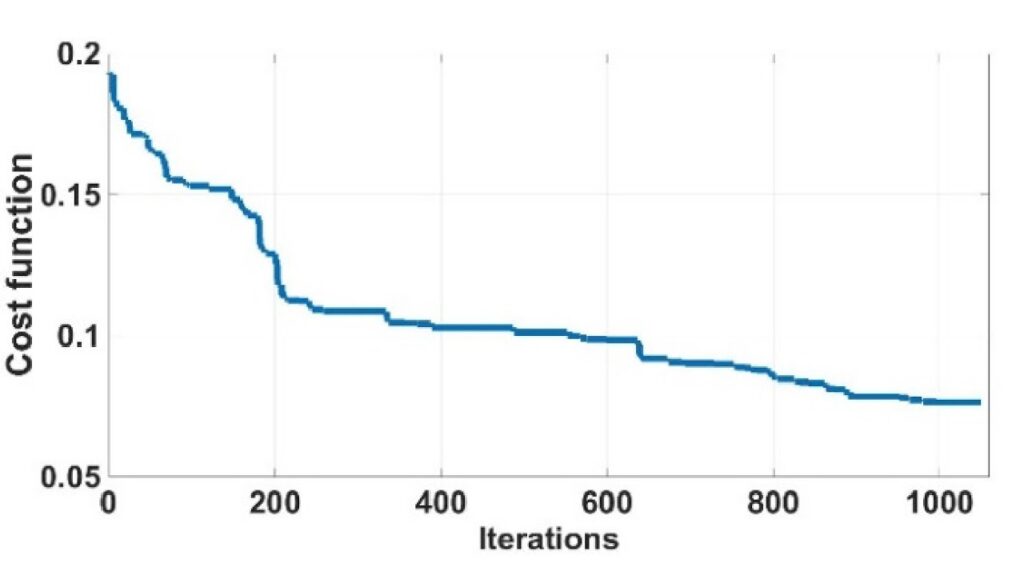
We use an optimization algorithm fed by data from a fast camera imaging the MMF output facet. From the observed intensity pattern, we compute a cost function based on the intensity correlation with a theoretical, desired eigenmode. Minimization of the cost function gives, within hundreds of seconds, the desired output mode as a result of the nonlinear dynamics with the appropriate initial modal power distribution (see Figs.1&2).

Recorded intensity patterns at the exit of the fiber for various excitations are shown on Fig. 3. They are similar to the profiles of the expected modes. Moreover, the output pattern obtained in wavevector space is also similar in shape to the near field intensity pattern for each selected mode. This information confirms the major contribution of the expected mode with a well-defined amplitude and phase distribution after the optimization of the launching conditions.

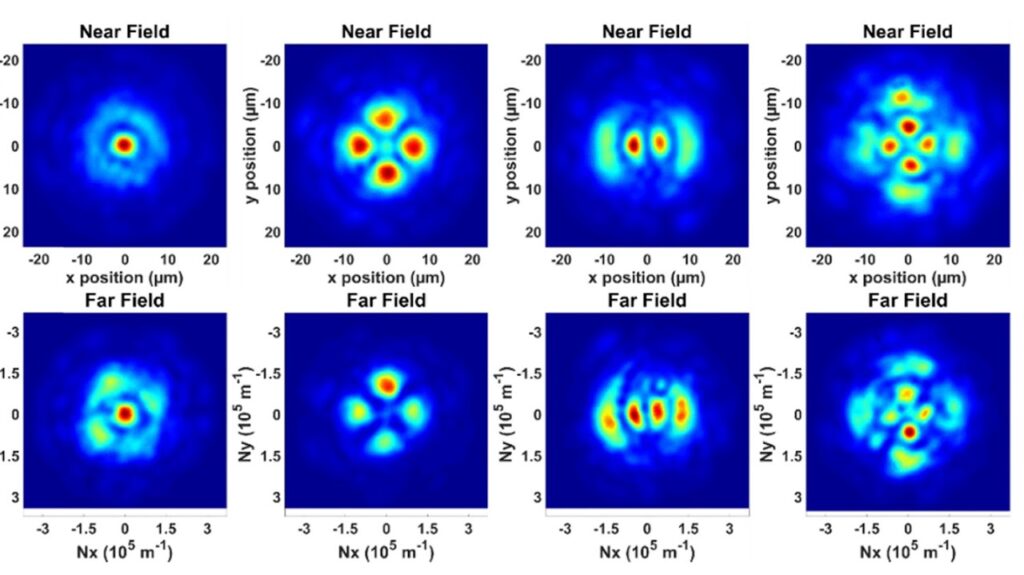
The nonlinear propagation regime is confirmed by a significant spectral broadening, and by the robustness of the Kerr beam self-cleaning. Whereas the adaptive process, in the linear propagation regime, simply pre- compensates linear mode coupling along the fiber, in order to structure a given intensity pattern onto its output facet. In contrast to the nonlinear regime, in the linear regime near and far fields are not identical. This shows that in the linear regime one generates a combination of modes, which maximizes intensity correlation with a target mode. To the contrary, Kerr nonlinearity plays a crucial role, by providing intermodal power exchanges which lead to highly efficient self-selection of a single, low-order mode on top of a background of higher-order modes.

1. I. M. Vellekoop and A. P. Mosk, “Focusing coherent light through opaque strongly scattering media,” Opt. Lett., vol. 32, no. 16, p. 2309, (2007)
2. H. Frostig et al., “Focusing light by wavefront shaping through disorder and nonlinearity,” vol. 4, no. 9, (2016)
3. O. Tzang et al., “Adaptive wavefront shaping for controlling nonlinear multimode interactions in optical fibres,” Nat. Photonics, vol. 12, no. 6, pp. 368–374, (2018)