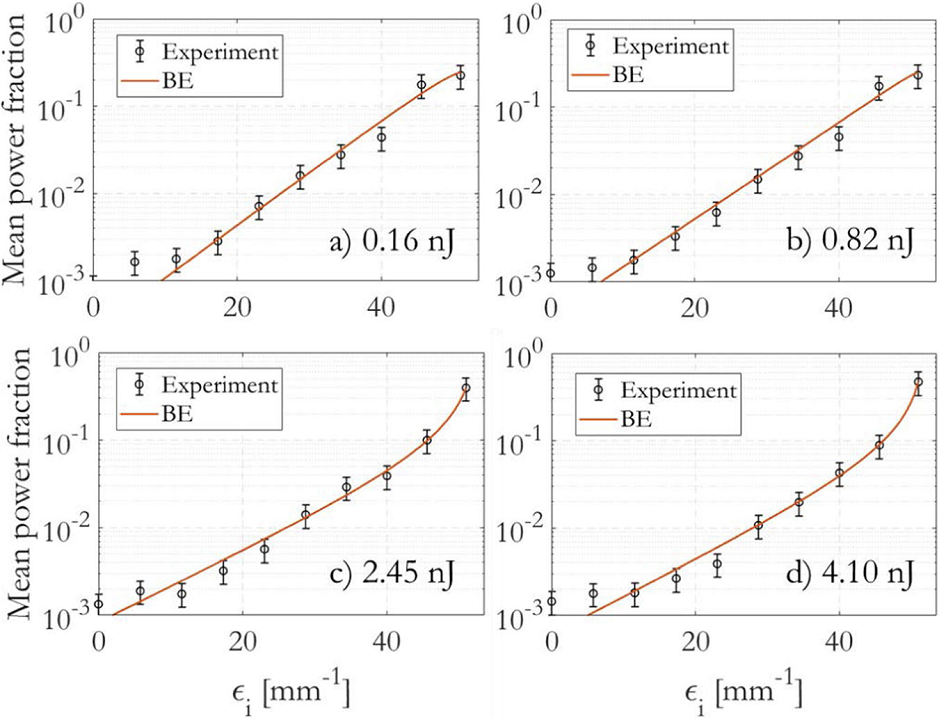
Optical pulses traveling through multimode optical fibers encounter the influence of both linear disturbances and nonlinearity, resulting in a complex and chaotic redistribution of power among different modes. In our research, we explore the phenomenon where multimode fibers reach stable states marked by the concentration of energy into both single and multiple subsystems. We introduce a weighted Bose-Einstein law, demonstrating its suitability in describing thermalized modal power distributions in the nonlinear regime, as well as steady-state distributions in the linear regime. We apply the law to experimental results and numerical simulations. Our findings reveal that, at power levels situated between the linear and soliton regimes, energy concentration occurs locally within higher-order modal groups before transitioning to global concentration in the fundamental mode within the soliton regime. This research broadens the application of thermodynamic principles to multimode fibers, uncovering previously unexplored optical states that exhibit characteristics akin to optical glass.
