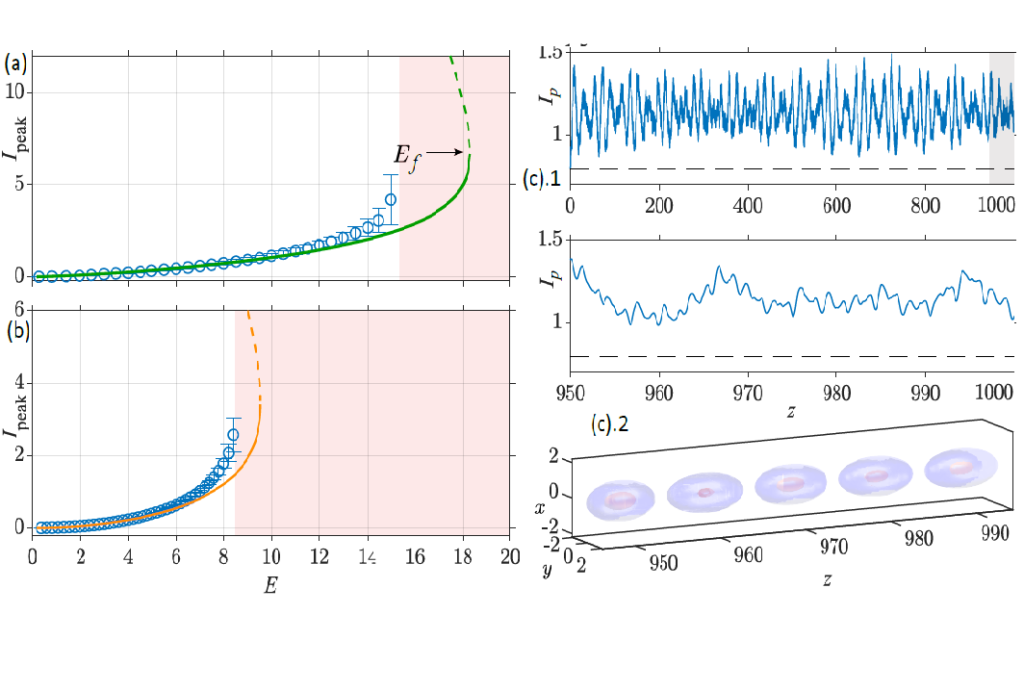
We analyze the formation of three-dimensional spatiotemporal solitons in waveguides with a parabolic refractive index profile and pure quartic chromatic dispersion. We show, by applying both variational approaches and full three-dimensional numerical simulations, that fourth-order dispersion has a positive impact on soliton stabilization against spatiotemporal wave collapse. Specifically, pure quartic spatiotemporal solitons remain stable within a significantly larger energy range with respect to their second-order dispersion counterparts
